Answer:
After 11 days,
32.37%.
Explanation:
We have been given that a percentage of the population infected t days after the disease arrives is approximated by
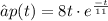 for
for
 .
.
In order to find the days when percentage of infected population is maximum, we will find critical values of the given function by setting its derivative equal to zero.
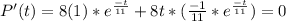

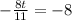
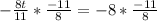
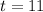
This is a critical value of the function. It can be the point of minimum or point of maximum. In order to check if it is a point of maximum, we will substitute this value of t in the second derivative (Second Derivative Test).
If we get the sign of second derivative as negative - then we will have a maximum at this value of t.
If we get the sign of second derivative as positive - then we will have a minimum at this value of t.


At
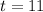 , we have second derivative negative as:
, we have second derivative negative as:
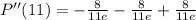
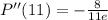
Therefore, we do have a maximum at
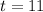 that is after 11 days the percentage of infected people is maximum.
that is after 11 days the percentage of infected people is maximum.
To find the maximum percentage, we need to substitute
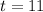 is the given function.
is the given function.
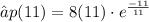
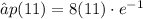
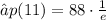
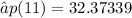
Therefore, 32.37% is the maximum percent of infected population.