Answer:
b. is described by all of these statements.
Step-by-step explanation:
Whenever a charge moves in a magnetic field it experiences a force upon it which is always perpendicular to the direction of its instantaneous velocity. The magnetic field causes the charged particles to change their direction of motion, but they do not change the speed of the particle (only the direction keeps changing).
This force was given first by H.A. Lorentz based on the extensive experiments of Ampere and others, hence it is called the Lorentz force.
Following are the factors that affect the magnetic force on a charged moving particle:
- The magnetic force is proportional to the charge "q" and to the magnitude of the vector cross product of the velocity of projection into the magnetic field and the intensity of the magnetic field.
- The cross product yields the result v.B sin∅ , where ∅ is the angle between the velocity and the direction of magnetic field lines.
- There will not be any magnetic force acting on the charge if it is projected parallel to the magnetic field lines, i.e. ∅=0° will yield sin∅=0.
- The direction of the magnetic force is opposite on a negatively charged particle than that on a positively charged particle.
- Magnetic force on a moving charge in a magnetic field is mathematically given as:
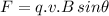
The attached image shows the Fleming's left hand rule to determine the direction of the force acting on the moving charge when the direction of moving charge and the direction of magnetic field are known. (In case of the movement of -ve charge take the opposite direction of actual movement)