Question

A hair dryer is basically a duct of constant diameter in which a few layers of electric resistors are placed. A small fan pulls the air in and forces it through the resistors where it is heated. If the density of air is 1.20 kg/m3 at the inlet and 0.955 kg/m3 at the exit, determine the percent increase in the velocity of air as it flows through the dryer.

Answer 1

the percent increase in the velocity of air is 25.65%

Step-by-step explanation:

Hello!

The first thing we must consider to solve this problem is the continuity equation that states that the amount of mass flow that enters a system is the same as what should come out.

m1=m2

Now remember that mass flow is given by the product of density, cross-sectional area and velocity

(α1)(V1)(A1)=(α2)(V2)(A2)

where

α=density

V=velocity

A=area

Now we can assume that the input and output areas are equal

(α1)(V1)=(α2)(V2)

`(V2)/(V1) =(\alpha1 )/(\alpha 2)`

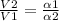
Now we can use the equation that defines the percentage of increase, in this case for speed

`i=((V2)/(V1) -1) 100`

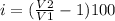
Now we use the equation obtained in the previous step, and replace values

`i=((\alpha1 )/(\alpha 2) -1) 100\\i=((1.2)/(0.955) -1) 100=25.65`

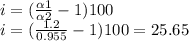
the percent increase in the velocity of air is 25.65%