Answer:
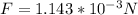 and
and
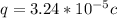
Step-by-step explanation:
a) We need first to identify the Period from the one-quarte 'time' given. That is
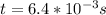
Then the period is,
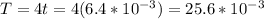
From this Period we can calculate the radio,

Rearrange for r,
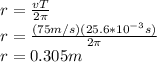
We know can calculate the Magnetic force,
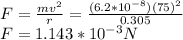
b) To find the charge we only use the Force in terms of the electric field, that is
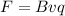
Rearrange to q,
