Question

Please help !!

Use the intermediate value theorem to choose the intervals over which the function, f(x)=x^4-2x^2-1, is guaranteed to have a zero. Select all that apply.

Answer 1

Explanation:

Since
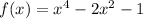`f(x)=x^4-2x^2-1` yields a smooth continuous curve (there's no x value where f(x) is undefined). We can apply intermediate value theorem here.

Substitute 0 for x and f(0) = 0 - 2*0 - 1 = -1 < 0

Substitute 2 for 2 and
`f(2) = 2^4 - 2*2^2 - 1 = 16 - 8 - 1 = 7 > 0`

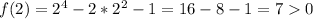
Since f(0) < 0 and f(2) > 0, by the intermediate value theorem, there's must be a point between 0 and 2 where the curve crosses the x axis (y = 0). Therefore this function is guaranteed to have a zero