Answer:
The correct answer is D
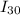 /
/
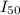 = 1.5
= 1.5
Step-by-step explanation:
In this exercise the moment of inertia equation should be used
I = ∫ r² dm
In addition to the parallel axis theorem
I =
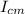 + M D²
+ M D²
Where
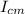 is the moment of the center of mass, M is the total mass of the body and D the distance from this point to the axis of interest
is the moment of the center of mass, M is the total mass of the body and D the distance from this point to the axis of interest
Let's apply these relationships to our problem, the center of mass of a uniform rod coincides with its geometric center, in this case the rod is 1 m long, so the center of mass is in
L = 100.00 cm (1m / 100 cm) = 1.0000 m
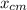 = 50 cm = 0.50 m
= 50 cm = 0.50 m
Let's calculate the moment of inertia for this point, suppose the rod is on the x-axis and use the concept of linear density
λ = M / L = dm / dx
dm = λ dx
Let's replace in the moment of inertia equation
I = ∫ x² ( λ dx)
We integrate
I = λ x³ / 3
We evaluate between the lower limits x = -L/2 to the upper limit x = L/2
I = λ/3 [(L/2)³ - (-L/2)³] = lam/3 [L³/8 - (-L³ / 8)]
I = λ/3 L³/4
I = 1/12 λ L³
Let's replace the linear density with its value
I = 1/12 (M/L) L³
I = 1/12 M L²
Let's calculate with the given values
I = 1/12 M 1²
I = 1/12 M
This point is the center of mass of the rod
Icm = I = 1/12 M = 8.333 10-2 M
Now let's use the parallel axis theorem to calculate the moment of resection of the new axis, which is 0.30 m from one end, in this case the distance is
D =
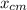 - x
- x
D = 0.50 - 0.30
D = 0.20 m
Let's calculate
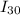 =
=
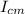 + M D²
+ M D²
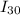 = 1/12 M + M 0.202
= 1/12 M + M 0.202
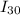 = M (1/12 + 0.04)
= M (1/12 + 0.04)
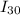 = M 0.123
= M 0.123
To find the relationship between the two moments of inertia, divide the quantities
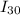 /
/
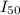 = M 0.123 / (M 8.3 10-2)
= M 0.123 / (M 8.3 10-2)
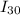 /
/
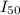 = 1.48
= 1.48
The correct answer is d 1.5