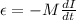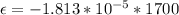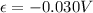Question

A solenoidal coil with 21 turns of wire is wound tightly around another coil with 350 turns. The inner solenoid is 25.0 cm long and has a diameter of 2.50 cm . At a certain time, the current in the inner solenoid is 0.120 A and is increasing at a rate of 1700 A/s. For this time, calculate;

(a) the average magnetic flux through each turn of the innersolenoid;
(b) the mutual inductance of the two solenoids;

Answer 1

A) We need to calculate the Magnetic flux of a Solenoid,

`\Phi = BA`

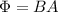
Where B is the magnetic field and A the Area.

`B=(\mu_0 N_2 I)/(l)`

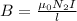
Here \mu_0 is the permeability constant, I the current and N number of turns.

Replacing we have,

`\Phi = (\mu_0 N_2 I)/(l)(\pi r^2)`

`\Phi = ((4\pi*10^(-7))(350)(0.12))/(25*10^(-2)) (\pi*(2.5*10^(-2))/(2)^2)`

`\Phi = 1.036*10^(-7)Wb`

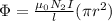
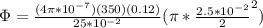
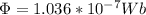
B) We calculate the mutual inductance, so

`M=(N_1 \Phi)/(i)`

`M=(21*1.036*10^(-7))/(0.12)`

`M=1.813*10^(-5)H`

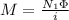
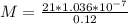
c) We calculate the emf

`\epsilon = -M (dI)/(dt)`

`\epsilon = -1.813*10^(-5)*1700`

`\epsilon= -0.030V`