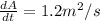Question

Two sides of a triangle are 8 m 8 m and 10 m 10 m in length and the angle between them is increasing at a rate of 0.06 rad/s 0.06 rad/s. Find the rate at which the area of the triangle is increasing when the angle between the sides of fixed length is π 3 rad π3 rad.

Answer 1

the rate at which the area of the triangle is increasing is
`1.2m^(2)/s`

Step-by-step explanation:

The area A of the triangle is given by:

A = (1/2)bh

Where b is the base of the triangle and h is the height of the triangle. if we know 2 sides of the triangle, we can define b and h using the attached image as:

b = 10 m

h = 8 sen(x)

Where x is the angle between the sides of fixed length. So the Area of the triangle is:

A = (1/2)(10)(8*sen(x))= 40*sen(x)

Then, if we derive the equation of the area with respect to the time, we get:

`(dA)/(dt) =40cos(x)(dx)/(dt)`

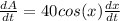
Where
`(dx)/(dt)` is the rate of the increasing angle.

So, if we replace this by 0.06 rad/s, we get:

`(dA)/(dt) =40cos(x)(0.06)`

`(dA)/(dt) =2.4cos(x)`

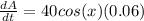
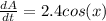
So, if x is equal to π/3, the rate at which the area of the triangle is increasing is:

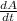`(dA)/(dt)`=2.4cos(π/3)

`(dA)/(dt) =1.2m^2/s`