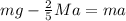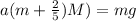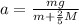Question

A uniform solid sphere of mass M and radius R is free to rotate about a horizontal axis through its center. A string is wrapped around the sphere and is attached to an object of mass m. Assume that the string does not slip on the sphere. (Use the following as necessary: M, m, and g.) Find the acceleration of the object.

Answer 1

`a = (mg)/(m + (2)/(5)M)`

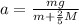
Step-by-step explanation:

To calculate the Acceleration and the tension of the object, we start by considering the value of the Tension through its moment of Inertia and Acceleration based on the angular velocity

`\tau = I\alpha = Tension(T)*R`

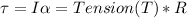
And
`a = \alpha R`

Replacing,

`T*R = I\alpha = ((2)/(5) MR^2)*(a)/(R))\\T*R = (2)/(5)MaR\\T = (2)/(5)Ma`

The following forces occur in the body,

`mg - T = ma`

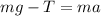
By this way we have the acceleration

`mg - (2)/(5)Ma = ma`

`a(m + (2)/(5))M) = mg`

`a = (mg)/(m + (2)/(5)M)`