Question

Rolle's theorem cannot be applied to the function f(x) = x1/3 on the interval [-1, 1] because

Answer 1

Answer with Step-by-step explanation:

We are given that a function

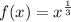`f(x)=x^{(1)/(3)}` on the interval [-1,1]

Rolle's theorem : It states that function is continuous on close interval [a,b] and differentiable on open interval (a,b) such that f(a)=f(b) , then

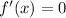`f'(x)=0` for some x
`a\leq x\leq b`

`a=-1 , b=1`

`f(1)=1`

`f(-1)=(-1)^{(1)/(3))=-1`

`f(-1)\\eq f(1)`

`f'(x)=\frac{1}{3x^{(2)/(3)}}`

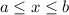
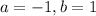
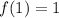
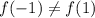
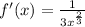
f is not differentiable at x=0.Therefore , f(x) is not diffrentiable on interval (-1,1)

Hence, Rolle's threorem cannot be applied for given function because it does not satisfied the condition of rolle's theorem.