Question

Again we have two methods, A and B, available for teaching a certain industrial skill. There is an 80% chance of successfully learning the skill if method A is used, and a 95% chance of success if method B is used. However, method B is substantially more expensive and is therefore used only 25% of the time (method A is used the other 75% of the time).A worker learned the skill successfully. What is the probability that he was taught by method A?

Answer 1

Given that the worker learned the skill succesfully, there is a 71.64% probability that he was taught by method A.

Explanation:

This can be formulated as the following problem:

What is the probability of B happening, knowing that A has happened.

It can be calculated by the following formula

`P = (P(B).P(A/B))/(P(A))`

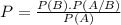
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.

In this problem, we have that:

What is the probability that the worker was taught by method A, given that he learned the skill successfully.

P(B) is the probability that he was taught by method A. Method A is used 75% of the time. So
`P(B) = 0.75`

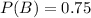
P(A/B) is the probability that he learned the skill succesfully, given that he was taught by method A. There is an 80% chance of successfully learning the skill if method A is used, so
`P(A/B) = 0.8`

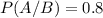
P(A) is the probability that he learned the skill succesfully. Method A is used 75% of the time and is 80% succesfull. Method B is used 25% and is 95% succesful. So

`P(A) = 0.75*0.8 + 0.25*0.95 = 0.8375`

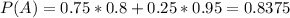
Finally

`P = (P(B).P(A/B))/(P(A)) = (0.75*0.8)/(0.8375) = 0.7164`

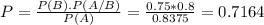
Given that the worker learned the skill succesfully, there is a 71.64% probability that he was taught by method A.