Question

A piece of cardboard measures 10 ft by 10 ft. Four equal squares of size x are removed from the corners. After removing the squares, the piece of cardboard is then folded into an open top box. What value of x would maximize its volume?

Answer 1

The value of x would be
`(5)/(3)`

Explanation:

Given,

The dimension of the cardboard = 10 ft by 10 ft,

∵ After removing four equal squares of size x ( in ft ) from the corners,

The dimension of the resultant box would be,

Length = ( 10 - 2x ) ft,

Width = ( 10 - 2x ) ft,

Height = x ft,

The volume of box,

`V=(10-2x)* (10 - 2x)* x=x(10-2x)^2 = x(100 - 40x + 4x^2)=100x - 40x^2 + 4x^3`

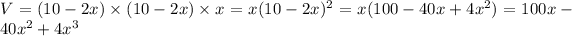
Differentiating with respect to x,

`V'=100 - 80x + 12x^2`

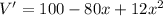
Again differentiating with respect to x,

`V''=-80 + 24x`

For maxima or minima,

`V'=0`

`\implies 100 - 80x + 12x^2 = 0`

`\implies 3x^2 - 20x + 25=0`

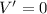
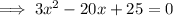
By quadratic formula,

`x=(20\pm √(20^2-4* 3* 25))/(6)`

`x=(20\pm √(400 - 300))/(6)`

`x=(20\pm √(100))/(6)`

`x=(20\pm 10)/(6)`

`\implies x = (10)/(6)=(5)/(3)\text{ or } x = 5`

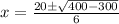
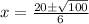
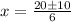
For x = 5/3, V'' = negative,

While for x = 5, V'' = Positive,

Hence, the value of x would be 5/3 ft for maximising the volume.