Question

Solve each system of equations by using substitution

Emily has a total of 20 dimes and nickels. If the dimes were nickels and nickels were dimes she would have 20 cents less than

she has now. How many of each coin does she have?

Answer 1

Emily has 12 dimes and 8 nickels.

Explanation:

Emily has a total of 20 coins.

Let d be the number of dimes she has and n the number of nickels:

`d + n = 20\\d= 20 - n`

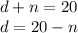
Dimes are worth 10 cents and nickels are worth 5 cents, therefore the amount she has and what she would have if the dimes were nickels and nickels were dimes are, respectively:

`d*10 + n*5\\d*5 + n*10`

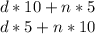
Since she would have 20 cents less in the second option, the following equation can be written:

`d*10 + n*5 = d*5 + n*10 + 20\\5(20-n) - 5n = 20`

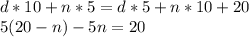
Substituting (d = 20 - n) into this equation yields:

`5(20-n) - 5n = 20\\10n=80\\n=8\\d=20 - 8\\d = 12`

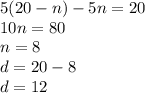
Emily has 12 dimes and 8 nickels.