Question

A tiny object carrying a charge of +40 μC and a second tiny charged object are initially very far apart. If it takes 49 J of work to bring them to a final configuration in which the +40 μC object i is atx = 1.00 mm, y = 1.00 mm, and the other charged object is at x = 1.00 mm, y = 3.00 mm (Cartesian coordinate system), find the magnitude of the charge on the second object. (k = 1/4πε 0 = 8.99 × 109 N · m2/C2)

a. 1.36 μC
b. 0.27 μC
c. 0.54 μC
d. 0.54 μC

Answer 1

Option b. 0.27 μC

Step-by-step explanation:

By definition, Coulomb's law quantifies the amount of force between two stationary, electrically charged particles:

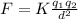`F= K(q_(1)q_(2))/(d^(2) )` (1)

To calculate q₂, we have to find the distances between the charges:

`d=\sqrt{(x_(2)-x_(1))^(2) + (y_(2)-y_(1))^(2)}` (2)

`d=\sqrt{(1-1)^(2) + (3-1)^(2)}`

`d=\sqrt{(0)^(2) + (2)^(2)}`

`d= 2 mm}`

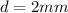
And now, we need to calculate the electrostatic force, by using the relation between force and electric potential:

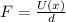`F= (U(x))/(d)` (3)

`F= (49J)/(2*10^(-3)m)`

`F= 24500 N}`

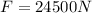
Finally, we calculate the magnitude of the charge on the second object, using the ecuation (1):

`F= K(q_(1)q_(2))/(d^(2) )`

`q_(2)=(F*d^(2))/(K*q_(1))`

`q_(2)=(24500N*(2*10^(-3)m)^(2))/(8.99*10^(9)Nm^(2)C^(-2)*40*10^(-6)C )`

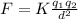
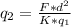
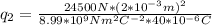
q₂ = 2.72 × 10⁻⁷C = 0.27 μC

So, the answer is the option b. q₂ = 0.27 μC

Have a nice day!