Question

The average ticket price for a concert at the opera house was $50. The average attendance was 4000. When the ticket price was raised to $52, attendance declined to an average of 3800 persons per performance. What should the ticket price be to maximize the revenue for the opera house?

Answer 1

given,

opera house ticket = $50

attendance = 4000 persons

now,

opera house ticket = $52

attendance = 3800 person

assuming these are the points on the demand curve

(x, p) = (4000,50) and (x,p) = (3800,52)

using point slope formula

`p-50 = (50-52)/(4000-3800)(x - 4000)`

`p-50 = (-2)/(200)(x - 4000)`

`p-50 = (-x)/(100)+ 40`

`p = (-x)/(100)+ 90`

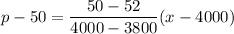
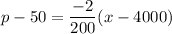
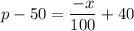
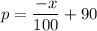
R(x) = x . p

`R(x) = x ((-x)/(100)+ 90)`

`R(x) = (-x^2)/(100)+ 90x)`

`(d)/(dx)(R(x)) = (d)/(dx)((-x^2)/(100)+ 90x))`

`(d)/(dx)(R(x)) = ((-2x)/(100))+90)`

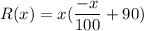
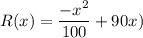
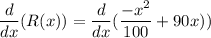
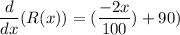
at
`(d)/(dx)(R(x)) = 0`

`(-2x)/(100)= -90`

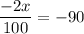
x = 4500

`(d^2)/(d^2x)(R(x)) = -ve`

hence at x =4500 the revenue is maximum

for maximum revenue ticket price will be

`p = (-4500)/(100)+ 90`

p = $45