Question

Suppose you need $50,000 ten years from now. you plan to make seven equal annual deposits with the first deposit to be made three years from today (e.g. t=3) in an account that yields 11% compounded annually. thus, your last deposit will be made at t=9. the money will remain in your account for one more year; it will continue to accrue interest, but you will not make at deposit at t=10. you will, however, withdraw $50,000 at that time. how much should each annual deposit be? (you might want to draw a time line to be sure you understand when the deposits are made.)

Answer 1

The installment will be for $ 4,148.010

Step-by-step explanation:

There will be 7 payment starting at the beginning of the third year therefore, an annuity-due. Then It will capitalize one more year.

Thus, the annuity future value will be the 50,000 discounted one year.

`(Nominal)/((1 + rate)^(time) ) = PV`

Nominal: 50,000.00

time: 1 year

rate: 11% = 11/100 = 0.11

`(50000)/((1 + 0.11)^(1) ) = PV`

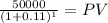
PV= 45,045.0450

Then we need to solve for the PMT of this annuity:

`FV / ((1+r)^(time) -1)/(rate)(1+r) = C\\`

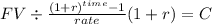
PV: $ 45,045

time: 7 years

rate: 11% = 11/100 = 0.11

`45045.045045045 / ((1+0.11)^(7) -1 )/(0.11)(1+0.11) = C\\`

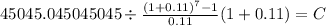
C $ 4,148.010