Answer:
a) There is a 66% probability that the selected review was submitted in Word format.
b)
If the selected review was submitted in Word format there is a 72.73% probability that it was short.
If the selected review was submitted in Word format there is a 22.73% probability that it was medium.
If the selected review was submitted in Word format there is a 4.54% probability that it was long.
Explanation:
We have these following probabilities:
A 60% probability that the review is short.
A 30% probability that the review is medium.
A 10% probability that the review is long.
If the review is short, a 80% probability that it was submitted in Word.
If the review is medium, a 50% probability that it was submitted in Word.
If the review is long, a 30% probability that it was submitted in Word.
(a) What is the probability that the selected review was submitted in Word format?
This is the sum of 90% of 60%, 50% of 30% and 30% of 10%.
So
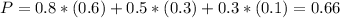
There is a 66% probability that the selected review was submitted in Word format.
(b)If the selected review was submitted in Word format, what are the posterior probabilities of it being short, medium, or long?
These questions can be formulated as the following question.
What is the probability of B happening, knowing that A has happened?
It can be calculated by the following formula
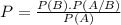
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.
Short
What is the probability that the review was short, given that it was submitted in Word format?
P(B) is the probability that the review is short. So
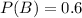
P(A/B) is the probability that the review was submitted in Word format, given that it was short. So
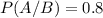 .
.
P(A) is the probability that the review was submitted in Word format. From a), we get that
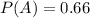 .
.
So:
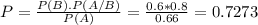
If the selected review was submitted in Word format there is a 72.73% probability that it was short.
Medium
What is the probability that the review was medium, given that it was submitted in Word format?
P(B) is the probability that the review is medium. So
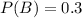
P(A/B) is the probability that the review was submitted in Word format, given that it was medium. So
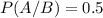 .
.
P(A) is the probability that the review was submitted in Word format. From a), we get that
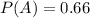 .
.
So:
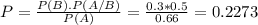
If the selected review was submitted in Word format there is a 22.73% probability that it was medium.
Long
What is the probability that the review was long, given that it was submitted in Word format?
P(B) is the probability that the review is long. So
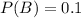
P(A/B) is the probability that the review was submitted in Word format, given that it was long. So
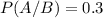 .
.
P(A) is the probability that the review was submitted in Word format. From a), we get that
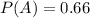 .
.
So:
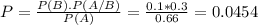
If the selected review was submitted in Word format there is a 4.54% probability that it was long.