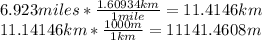Question

A hot-air balloon is floating above a straight road. To calculate their height above the ground, the balloonists simultaneously measure the angle of depression to two consecutive mileposts on the road on the same side of the balloon. The angles of depression are found to be 24∘ and 27∘.

Answer 1

Height of the balloon is 6.923 miles or 11141.46m

Step-by-step explanation:

We form two triangles with a common vertex so the relation of the angles is and the position both are measuring

`tan(27)=(Op)/(Ad)\\Op1=Ad*Tan(27)\\Op1=Ad*0.595`

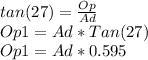
The second triangle have the mileposts on the road that is a mile more so:

`tan(24)=(Op)/(Ad+1mile) \\Op=tan(24)*(Ad+1mile)\\Op=0.445*(Ad+1mile)`

`Op=0.445*Ad+0.445`

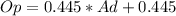
Now resolve the both equation to know the opposite side that is the height of the hot air balloon

`Op*0.595=Op*0.4452+0.4452\\Op*(0.595-0.4452)=0.4452\\Op*0.0643=0.4452\\Op=(0.4452)/(0.0643)`

`Op=6.923 mile`

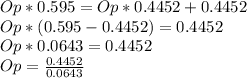
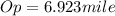
Height=6.923miles

Leigth can be find also

`Ad=tan(27)*6.923\\Ad=3.52 miles`

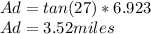
The measure can be express in meters so

`6.923miles*(1.60934km)/(1mile)=11.4146km\\11.14146km*(1000m)/(1km)=11141.4608 m`