Question

If the coefficient of friction is 0.3900 and the cylinder has a radius of 2.700 m, what is the minimum angular speed of the cylinder so that the people don't fall out? (Normally the operator runs it considerably faster as a safety measure.)

Answer 1

w=3.05 rad/s or 29.88rpm

Step-by-step explanation:

k = coefficient of friction = 0.3900

R = radius of the cylinder = 2.7m

V = linear speed of rotation of the cylinder

w = angular speed = V/R or to rewrite V = w*R

N = normal force to cylinder

N=
`=(m(V)^(2))/(R)=m*(w)^2*R`

`Friction force\\Ff = k*N\\Ff= k*m*w^2*R`

`Gravitational force \\Fg = m*g`

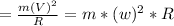
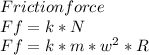
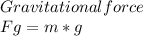
These must be balanced (the net force on the people will be 0) so set them equal to each other.

`Fg = Ff`

`m*g = k*m*w^2*R`

`g=k*w^(2)*R`

`w^2 =(g)/(k*R)`

`w=\sqrt{(g)/(k*R)} \\w =\sqrt{(9.8(m)/(s^(2)))/(0.3900*2.7m)}\\ w=√(9.306)=3.05 (rad)/(s)`

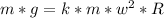
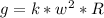
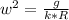
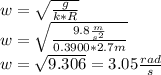
There are 2*pi radians in 1 revolution so:

`RPM=(w)/(2\pi )*60\\RPM=(3.05(rad)/(s))/(2\pi)*60\\RPM= 0.498*60\\RPM=29.88`

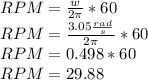
So you need about 30 RPM to keep people from falling out the bottom