Question

The correlation coefficient between two quantitative variables is approximately 0.6. What does the value of this correlation coefficient indicate about how well the model fits the data?

Answer 1

The model does not fits the data well.

Explanation:

Correlation:

• Correlation is a technique that help us to find or define a relationship between two variables.

• It is a measure of linear relationship between two quantities.

• A positive correlation means that an increase in one quantity leads to an increase in another quantity
• A negative correlation means with increase in one quantity the other quantity decreases.

R-square,
`R^2`

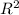
• The quantity R-squared is an indicator of the predictive power of a model.
• It explains the variation in the dependent variable due to independent variable.
• It shows how well the model fits the data.
• R-squared is also known as the coefficient of determination.

`R^2 = \text{(Correlation coefficient)}^2= (0.6)^2 = 0.36 = 36\%`

Therefore, only 36% of the variations in the dependent variable is explained by the independent variable in the model which means more than 50% of variation cannot still be explained in the dependent variable.

Hence, the model does not fits the data well.