Question

The expression 3p2 represents the number of ways of:

a. choosing 2 items at a time from a set of 3.

c. arranging, in order, 2

Answer 1

Answer:C

Explanation:

I took the test on edge.

Answer 2

c.Arranging in order 2 from a set of 3.

Explanation:

We are given that an expression

`3P_2`

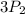
Permutation : permutation is an arrangement of of n items when r items taken at a time.

It is represented as
`nP_r`

`nP_r=(n!)/(r!(n-r)!)`

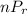
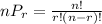
Combination is a selection of r items at a time out of n items.

It is represented by
`nC_r=(n!)/(r!(n-r)!)`

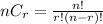
Therefore, the given expression represents the number of number of ways of arranging in order 2 from a set of 3.

Answer:c.Arranging in order 2 from a set of 3.