Answer:
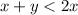
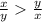
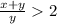
Explanation:
For solving the question first we need to revise the properties of inequality,
a < b ⇒ a ± c < b ± c ∀ a, b, c ∈ R,
a < b ⇒ ca < cb if c > 0,
a < b ⇒ ca > cb if c < 0
Part 1 :
Given,
x and y are two numbers ( must be positive real numbers because they are showing the heights )
Such that, x > y,
Adding x on both sides of the inequality,
x + x > y + x
2x > y + x
⇒ x + y < 2x
Thus, SECOND option is correct.
Part 2 :
∵ x > 0 ⇒ 1/x > 0,
x > y
⇒


Similarly, y > 0 ⇒ 1/y > 0

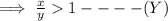
From equation (X) and (Y),
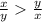
Thus, FIRST option is correct.
Part 3 :
Now, x > y
x + y > 2y
Since, y > 0 ⇒
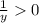
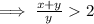
Thus, FIRST option is correct.