Question

The mean of a normal probability distribution is 460; the standard deviation is 18.About 68% of the observations lie between what two values?About 95% of the observations lie between what two values?Practically all of the observations lie between what two values?

Answer 1

Answer with explanation:

As per given , we have

`\mu=460` ,
`\sigma= 18`

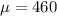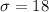
• According to the empirical rule , about 68% of the population lies within 1 standard deviation from mean :-

i.e. About 68% of the observations lie between (
`\mu-1(\sigma)` and
`\mu+1(\sigma)`)

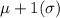i.e. About 68% of the observations lie between (
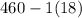`460-1(18)` and
`460+1(18)`)

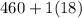About 68% of the observations lie between 442 and 478.

• Again , according to the empirical rule , about 95% of the population lies within 2 standard deviations from mean :-

i.e. About 95% of the observations lie between (
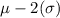`\mu-2(\sigma)` and
`\mu+2(\sigma)`)

i.e. About 95% of the observations lie between (
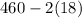`460-2(18)` and
`460+2(18)`)

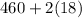About 95% of the observations lie between 424 and 496.

• Also, Practically all of the observations(99.7%) lie between lies within 3 standard deviations from mean :-

i.e. Practically all of the observations lie between (
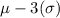`\mu-3(\sigma)` and
`\mu+3(\sigma)`)

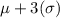i.e. Practically all of the observations lie between (
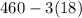`460-3(18)` and
`460+3(18)`)

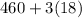Practically all of the observations lie between 406 and 514.