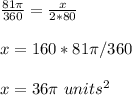Question

The measure of central angle YCZ is 80 degrees. Circle C is shown. Line segments X C, W C, Y C, and Z C are radii. The length of X C is 9. Angle Y C Z is 80 degrees. Sectors X C W and Y C Z are shaded. What is the sum of the areas of the two shaded sectors? 18 units2 36 units2 45 units2 81 units2

Answer 1

b would be the right option

Explanation:

Answer 2

The sum of the areas of the two shaded sectors is
`36\pi\ units^(2)`

Explanation:

see the attached figure to better understand the problem

we know that

The area of a circle is equal to

`A=\pi r^(2)`

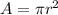
where

r is the radius of the circle

in this problem we have

`r=9\ units`

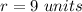
substitute

`A=\pi (9)^(2)=81 \pi\ units^(2)`

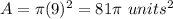
Remember that

`360\°` subtends the complete circle of area equal to
`81 \pi\ units^(2)`

so

By proportion

Find the area of the two shaded sectors

`(81\pi )/(360)=(x)/(2*80)\\ \\x=160*81\pi/360\\ \\x=36\pi\ units^(2)`