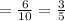Question

The number $n$ is randomly selected from the set $\{1, 2,\ldots, 10\}$, with each number being equally likely. What is the probability that $2n - 4 > n$?

Answer 1

The probability is 3/8

Explanation:

Of the eight possible outcomes, there are three successful ones: HHH, HHT, and THH, so, the probability is 3/8

Answer 2

The probability would be 3/5

Explanation:

Here,

n ∈ { 1, 2, ..........., 10}

Also, the given inequality,

2n - 4 > n

By using a > b ⇒ a ± c > b ± c ∀ a, b, c ∈ R,

2n - 4 - n > 0

n - 4 > 0

n > 4,

Thus, the numbers which are following the given inequality are,

{5, 6, 7, 8, 9, 10}

Now,

`\text{Probability}=\frac{\text{Favourable outcomes}}{\text{Total outcomes}}`

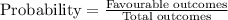
Since, numbers which are more than 4 = 6,

Total numbers = 10,

Hence, the probability that 2n - 4 > n

`=(6)/(10)=(3)/(5)`