Question

Two satellites orbit the earth in stable orbits. Satellite a is three times the mass of satellite b. Satellite a orbits with a speed v at a distance r from the center of the earth. Satellite b travels at a speed that is greater than v. At what distance from the center of the earth does the satellite b orbit?

Answer 1

Radius of satellite b will be smaller than the radius of satellite a.

Step-by-step explanation:

m = Mass of satellite

v = Velocity of satellite

r = Radius of satellite orbit

Equating centripetal force and Gravitational force

`(mv^2)/(r)=(GmM)/(r^2)`

`\\\Rightarrow (v^2)/(r)=(GM)/(r^2)`

`\\\Rightarrow v^2=(GM)/(r)`

`\\\Rightarrow v=sqrt{GM/r}`

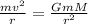
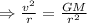
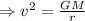
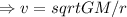
It can be seen that the velocity is inversely proportional to the radius and the mass of the satellite does not have any effect.

This means that in order for v to increase the radius has to decrease

Here,
`v_b>v_a`

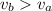
So, the radius of satellite b will be smaller than the radius of satellite a.