Answer:
13.8
Explanation:
We are given that
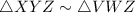
When two triangles are similar then
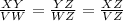
WZ=15 , ZY=12
XY=11
We have to find the WV.
Substitute the values then we get
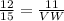
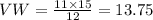
We have to round to the nearest tenth of final answer.
The Hundredth place =5 which is equal to 5.Therefore, 1 will be added tenth place 7 and all digits on left side remain same and digit on right side of tenth place replace by zero.
Therefore, WV=13.8