Answer:
A)
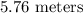
B) 62
Explanation:
The width of a red blood cell is approximately 8 micrometers
 meters
meters
Part A)
Width of 1 red blood cell
 meters
meters
width of
 red blood cells
red blood cells
 meters
meters

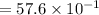
Now change into scientific notation. So, decimal should be between 1 to 10
Decimal move 1 digit right to left
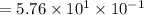
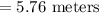
Hence, the width of red blood cells is
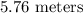
Part B)
If a grain of salt is 0.5 mm wide.
First convert mm to m. ( 1 mm = 1 × 10⁻³ m)
Therefore, 0.5 mm = 5 × 10⁻⁴ m

Size of a grain = 5 × 10⁻⁴ m
Size of a blood cell = 8 × 10⁻⁶ m
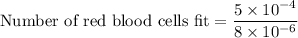
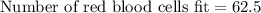
Hence, 62 number of red blood cells fit in a grain of salt.