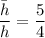Question

In an experiment, the local heat transfer over a flat plate were correlated in the form of local Nusselt number as expressed by the correlation Nux=0.035Rex^(0.8) Pr^(1/3) Determine the ratio of the average convection heat transfer coefficient (h) over the entire plate length to the local convection heat transfer coefficient (hx) (h/hx = L) at x = L.

Answer 1

`\frac{\bar{h}}{h}=(5)/(4)`

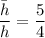
Step-by-step explanation:

Given that

`Nu_x=0.035Re_x^(0.8) Pr^(1/3)`

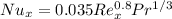
We know that

Rex=ρvx/μ

So

`Nu_x=0.035Re_x^(0.8) Pr^(1/3)`

`Nu_x=0.035*\left((\rho vx)/(\mu)\right)^(0.8)Pr^(1/3)`

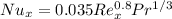
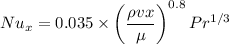
All other quantities are constant only x is a variable in the above equation .so lets take all other quantities as a constant C

`Nu_x=C.x^(0.8)=C.x^(4/5)`

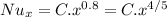
We also know that

Nux=hx/K

`C.x^(4/5)=(hx)/(k)`

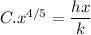
m is the constant

`h=mx^(-1/5)`

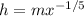
This is local heat transfer coefficient

The average value of h given as

`\bar{h}=(\int_(0)^(L)hdx)/(L)`

`\bar{h}=(5m)/(4)*(L^(4/5))/(L)`

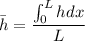
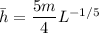`\bar{h}=(5m)/(4)L^(-1/5)` ---------1

The value of local heat transfer coefficient at x=L

`h=mx^(-1/5)`

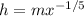
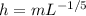`h=mL^(-1/5)` -----------2

From 1 and 2 we can say that

`\frac{\bar{h}}{h}=(5)/(4)`