Question

Triangle A has a height of 2.5\text{ cm}2.5 cm2, point, 5, start text, space, c, m, end text and a base of 1.6\text{ cm}1.6 cm1, point, 6, start text, space, c, m, end text. The height and base of triangle B are proportional to the height and base of triangle A

Answer 1

A, D, E

Explanation:

Khan Academy

Answer 2

A)Height: 2.75 CM

Base: 1.76 CM

D)Height: 1.25 cm

Base:0.8 cm

E) height: 2 cm

base: 1.28 cm

Explanation:

The complete question is

Triangle A has a height of 2.5 cm and a base of 1.6 cm The height and base of triangle B are proportional to the height and base of triangle A.

Which of the following could be the height and base of triangle B?

Choose 3 answers:

A)Height: 2.75 CM

Base: 1.76 CM

B) Height :9.25 cm

Base:9.16 cm

C)Height: 3.2 cm

base: 5 cm

D)Height: 1.25 cm

Base:0.8 cm

E) height: 2 cm

base: 1.28 cm

we know that

If the height and base of triangle B are proportional to the height and base of triangle A, then their ratios of the height to the base must be equal

step 1

Find out the ratio of the height to the base of triangle A

so

`(2.5)/(1.6)= 1.5625`

step 2

Verify the ratio of the height to the base of each case and then compare with ratio of triangle A

A)Height: 2.75 CM

Base: 1.76 CM

`(2.75)/(1.76)= 1.5625`

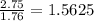
Compare

`1.5625= 1.5625`

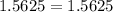
therefore

Could be the height and base of triangle B

B) Height :9.25 cm

Base:9.16 cm

`(9.25)/(9.16)= 1.0098`

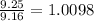
Compare

`1.0098 \\eq 1.5625`

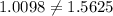
therefore

It couldn't be the height and base of the B triangle.

C) Height: 3.2 cm

base: 5 cm

`(3.2)/(5)= 0.64`

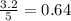
Compare

`0.64 \\eq 1.5625`

therefore

It couldn't be the height and base of the B triangle.

D)Height: 1.25 cm

Base:0.8 cm

`(1.25)/(0.8)= 1.5625`

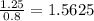
Compare

`1.5625= 1.5625`

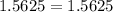
therefore

Could be the height and base of triangle B

E) height: 2 cm

base: 1.28 cm

`(2)/(1.28)= 1.5625`

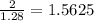
Compare

`1.5625= 1.5625`

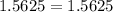
therefore

Could be the height and base of triangle B