Question

Two angles are given.

m<g = (2x - 90)
m<h = (180 - 2x)
Which statements are true about <g and <h if both angles are greater than zero.​

Answer 1

A and C

Explanation:

Answer 2

Angle g and h are complementary angles.

Angle g and h are acute angles.

Explanation:

The given angles are

`m\angle g=(2x-90)^(\circ)`

`m\angle h=(180-2x)^(\circ)`

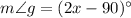
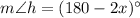
If sum of two angles is 180, then they called supplementary angles.

If sum of two angles is 90, then they called complimentary angles.

Add both angles.

`m\angle g+m\angle h=(2x-90)^(\circ)+(180-2x)^(\circ)`

`m\angle g+m\angle h=(2x-90+180-2x)^(\circ)`

`m\angle g+m\angle h=90^(\circ)`

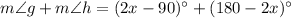
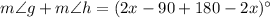
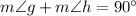
The sum of two angles is 90 degree, therefore angle g and h are complementary angles.

Both angles are greater than zero and their sum is 90, it means

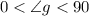`0<\angle g<90` and
`0<\angle h<90`

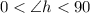
Therefore, angle g and h are acute angles.