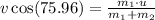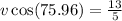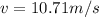Question

2) Two vehicles approach a right angle intersection and then collide. After the collision, they become entangled. If their mass ratios were 1: 4 and their respective speeds as they approached were both 13 m/s, find the magnitude and direction of the final velocity of the wreck.

Answer 1

Answer:
`10.71 m/s at angle of 75.96^(\circ)`

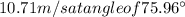
Step-by-step explanation:

Given

Given two vehicles approach a right angle

Suppose one is traveling with towards north and other towards east

Ratio of their masses is
`(m_1)/(m_2)=(1)/(4)`

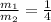
Both have a common velocity(u) of 13 m/s and v be the final velocity at an angle of
`\theta`w.r.t to east after collision

after collision they both entangled thus

conserving Momentum in east i.e horizontal direction

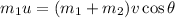`m_1u=(m_1+m_2)v\cos \theta`---1

conserving momentum in North direction i.e. in vertical direction

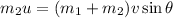`m_2u=(m_1+m_2)v\sin \theta`---2

Divide 1 &2 we get

`(m_1)/(m_2)=(\cos \theta )/(\sin \theta )`

`\tan \theta =(m_2)/(m_1)`

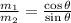
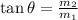
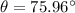`\theta =75.96^(\circ)` w.r.t east

Thus v is given by

`v\cos (75.96)=(m_1\cdot u)/(m_1+m_2)`

`v\cos (75.96)=(u)/(1+4)`

`v\cos (75.96)=(13)/(5)`

`v=10.71 m/s`