Answer: Estimated standard error for the sample mean difference would be 1.
Explanation:
Since we have given that
Mean of MD = 4.90
So, Sum of difference would be

S = 288
n = 9
We need to find the standard error for the sample mean differences.
Estimated standard error for the sampled mean difference would be
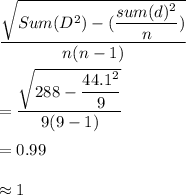
Hence, estimated standard error for the sample mean difference would be 1.