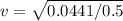Answer:
v= 0.9391m/s
Step-by-step explanation:
We apply conservative energy equation, where all the work done by all forces is equal to change in Kinetic Energy.
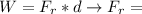 Frictional Force
Frictional Force
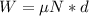
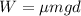

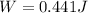
The change in Kinetic Energy is given by,

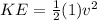
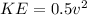
How the work done by all force is equal to the change in KE, we have that
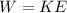

Solving v,