Question

Meow Cat chow has a demand of 4000 units per year. When producing the product, the factory's setup cost is $20, and holding cost is $4 per unit per year. The cost-minimizing solution for this product is to order:

(A) all 4000 units at one time.
(B) 200 units per order.
(C) every 20 days.
(D) 10 times per year.
(E) none of the above

Answer 1

(B) 200 units per order.

Step-by-step explanation:

With the economic order quantity formula we can solve for the minimum invnetory cost:

`Q_(opt) = \sqrt{(2DS)/(H)}`

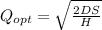
Where:

D = annual demand = 4,000

S= setup cost = ordering cost = 20

H= Holding Cost = 4.00

`Q_(opt) = \sqrt{(2(4,000)(20))/(4)}`

`Q_(opt) = \sqrt{(160,000)/(4)}`

`Q_(opt) = √(40,000)`

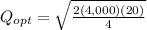
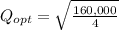
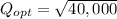
EOC = 200 units