Question

Can someone help me find the functions zeros

Answer 1

(5,0) or (1,0)

Explanation:

1.) First you distribute the parenthesis (as it goes first in the PEMDAS series)

`2(x-3)^(2) -8=2(x-3)(x-3)-8= 2(x^(2) -6x+9)-8`

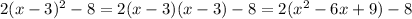
2.) Distribute the 2 into the expression in the parenthesis and simplify

`2(x^(2) -6x+9)-8=2x^(2) -12x+18-8=\\2x^(2) -6x+10=g(x)`

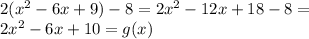
3.) Factor the quadratic

(there is many ways for different equations, so it is hard to explain how to, maybe go online if you are struggling, that's how I do mine)

`2x^(2) -12x+10=2(x-5)(x-1)=0`

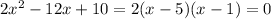
(Editors note: reason why we must put zero to solve for the functions zero is because we must find the "X" when "Y=0", or in this case "g(x)=0")

4.) Separate each of the parenthesis that you factored from the equation into two equations and solve for x when g(x)=0

`2(x-5)=0\\2x-10=0\\2x=10\\(2x)/((2)) =(10)/((2)) \\x=5`

`(x-1)=0\\x=1`

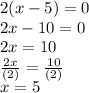
So when y=0, x=5 or 1

5.) Turn the x and y values given into point form

(x=5,1) (y=0) so... (5,0) and (1,0)

Answer 2

`\bf g(x) = 2(x-3)^2-8\implies \stackrel{g(x)}{0}=2(x-3)^2-8\implies 8=2(x-3)^2 \\\\\\ \cfrac{8}{2}=(x-3)^2\implies 4=(x-3)^2\implies \pm√(4)=x-3\implies \pm 2 = x-3 \\\\\\ \pm 2 +3 = x\implies x = \begin{cases} 5\\ 1 \end{cases}`