Answer:
4.7 units
Explanation:
We are given that in triangle ABC
AB= 3 units
Angle ABC=76 degree
Angle CAB=66 degrees
AC=b
We have to find the approximate value of b using sin laws.
We know that sum of angles of a triangle =180 degrees
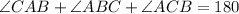
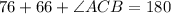
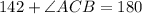

We know that law of sines
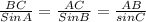
Substitute the values then we get
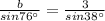
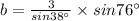
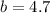
Hence, the value of b= 4.7 units