Answer:
Option 4, SAS
Explanation:
Given information: BL=PF, BG=PX and m∠LBG=m∠FPX.
In triangle BLG and triangle PFX,
BL=PF (Given)
m∠LBG=m∠FPX (Given)
BG=PX (Given)
Two triangles are congruent if two corresponding sides and included angle are congruent.
Two sides and the included angle of triangle BLG are equal to two sides and the included angle of another triangle PFX. By SAS postulate we can say that
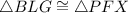 (By SAS)
(By SAS)
Therefore, the correct option is 4.