Question

What is the range of f(x) = (three-fourths) Superscript x – 4?

y > –4



Left-brace y vertical line y greater-than three-fourths right-brace



y < –4



Left-brace y vertical line y less-than three-fourths right-brace

Answer 1

Option 1 -
`\y>-4\`

Explanation:

Given : Function
`f(x)=((3)/(4))^x-4`

To find : What is the range of f(x) ?

Solution :

Function
`f(x)=((3)/(4))^x-4`

We put some value of x to determine the range,

For x=-1,

`f(0)=((3)/(4))^(-1)-4=0.33`

For x=0,

`f(0)=((3)/(4))^0-4=-4`

For x=1,

`f(0)=((3)/(4))^1-4=-0.25`

For x=2,

`f(0)=((3)/(4))^2-4=-0.4375`

As we see that, the value of y is greater than -4.

Therefore, the range of the function is
`\y>-4\`

So, Option 1 is correct.

Answer 2

Option A.

Explanation:

The given function is

`f(x)=(3)/(4)^(x)-4`

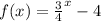
We need to find the range of f(x).

The given function can be rewritten as

`y=(3)/(4)^(x)-4`

Range is the set of output values.

If
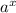`a^x`, where a>0, then the value of
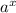`a^x` is always greater than 0.

Using the above property, we get

`(3)/(4)^(x)>0`

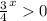
Subtract 4 from both sides.

`(3)/(4)^(x)-4>0-4`

`y>-4`

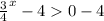
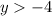
Range = y

Therefore, the correct option is A.