Question

A plane flies horizontally with a speed of 600 km/h at an altitude of 10 km and passes directly over the own of Quinton. Find the rate at which the distance from the plane to Quinton is increasing when it is 20 km away from Quinton

Answer 1

86.6 km/h

Step-by-step explanation:

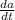`(da)/(dt)` = Velocity of Plane = 600 km/h

a = Distance Plane travels

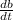`(db)/(dt)` = Vertical velocity of Plane = 0

b = Altitude of plane = 10 km

c = Distance between town and plane = 20 km

`a=√(c^2-b^2)\\\Rightarrow a=√(20^2-10^2)\\\Rightarrow a=17.32\ km`

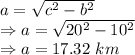
From Pythogoras theorem

a²+b² = c²

Now, differentiating with respect to time

`2a(da)/(dt)+2b(db)/(dt)=2c(dc)/(dt)\\\Rightarrow a(da)/(dt)+b(db)/(dt)=c(dc)/(dt)\\\Rightarrow (dc)/(dt)=(a(da)/(dt)+b(db)/(dt))/(c)\\\Rightarrow (dc)/(dt)=(17.32* 100+10* 0)/(20)\\\Rightarrow (dc)/(dt)=86.6\ km/h`

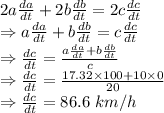
The rate at which the distance from the plane to Quinton is increasing 86.6 km/h