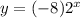Answer:
Explanation:
The exponential function will have this form:
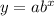
We know that the function passes through the points
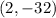 and
and
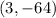 . Then, we can substitute the coordinates of the point
. Then, we can substitute the coordinates of the point
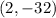 into
into
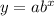 and solve for "a":
and solve for "a":
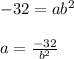
Then, we know that:
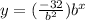
Now, we neeed to substitute the coordinates of the second point
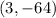 into
into
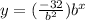 and solve for "b":
and solve for "b":
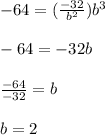
Substituting the value of "b" into
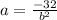 we can find "a":
we can find "a":
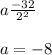
Therefore, we get that the exponential function that describes the graph, is: