Answer:
a) - r=5%:
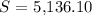
- r=4%:
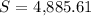
- r=3%:
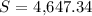
b) - r=5%: t=14 years
- r=4%: t=17 years [/tex]
- r=3%: t=23 years [/tex]
c) The amount obtained is
- Compuonded quarterly: $5,191.83
- Compuonded continously: $5,200.71
The latter is always greater, since the more often it is capitalized, the greater the effect of compound interest and the greater the capital that ends up accumulating.
Step-by-step explanation:
The rate of accumulation of money is
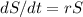
To calculate the amount of money accumulted in a period, we have to rearrange and integrate:
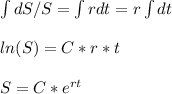
When t=0, S=S₀ (the initial capital).
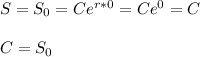
Now we have the equation for the capital in function of time:
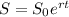
a) For an initial capital of $4000 and for a period of five years, the amount of capital accumulated for this interest rates is:
- r=5%:
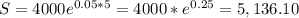
- r=4%:
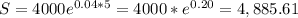
- r=3%:
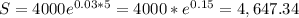
b) We can express this as
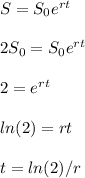
- r=5%:
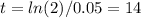
- r=4%:
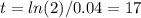
- r=3%:
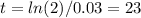
c) When the interest is compuonded quarterly, the anual period is divided by 4. In 5 years, there are 4*5=20 periods of capitalization. The annual rate r=0.0525 to calculate the interest is also divided by 4:
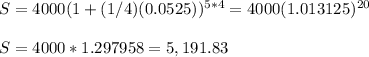
If compuonded continously, we have:
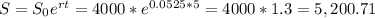
The amount obtained is
- Compuonded quarterly: $5,191.83
- Compuonded continously: $5,200.71
The latter is always greater, since the more often it is capitalized, the greater the effect of compound interest and the greater the capital that ends up accumulating.