Question

Sanjana jogged uphill for a while at an average speed of 3 miles per hour, then jogged downhill for a while at an average speed of 8 miles per hour. If Sanjana jogged the uphill and downhill stretches in a total of 40 minutes at an average speed of 4 miles per hour, how far did she jog uphill?

Answer 1

She jogged uphill for 1.6 miles

Explanation:

Given:

Uphill speed = 3 miles per hour

Downhill speed = 8 miles per hour

Total time to cover uphill and downhill = 40 minutes =
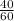`(40)/(60)` hours

Average speed = 4 miles per hour

Now,

Let the distance of uphill be 'x'

and downhill distance be 'y'

Time =
`\frac{\textup{Distance}}{\textup{Speed}}`

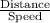
therefore,

`(x)/(3)+(y)/(8)=(40)/(60)`

or

`(8x+3y)/(3*8)=(2)/(3)`

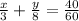
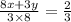
or

8x + 3y = 16 ...........(1)

also,

Average speed =
`\frac{\textup{Total distance}}{\textup{Total time}}`

or

4 =
`\frac{\textup{x+y}}{(40)/(60)}`

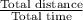
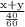
or

4 × 40 = 60(x + y)

or

3x + 3y = 8

or

3y = 8 - 3x ............(2)

substituting 2 in 1, we get

8x + (8 - 3x) = 16

or

5x + 8 = 16

or

5x = 8

or

x = 1.6 miles

and,

3y = 8 - 3x

or

3y = 8 - 3(1.6)

or

3y = 8 - 4.8

or

y = 1.067 miles

Hence,

She jogged uphill for 1.6 miles