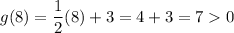Question

Need help! a.s.a.p! please!

Answer 1

`\large\boxed{y=(1)/(2)x-2}\\\boxed{f(8)=2}\\\boxed{\text{positive}}`

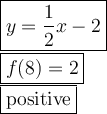
Explanation:

The slope-intercept form of an equation of a line:

`y=mx+b`

m - slope

b - y-intercept → (0, b)

The fromula of a slope:

`m=(y_2-y_1)/(x_2-x_1)`

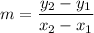
From the graph we hate x-intercept (4, 0) and y-intercept (0, -2) → b = -2

Calculate the slope:

`m=(-2-0)/(0-4)=(-2)/(-4)=(1)/(2)`

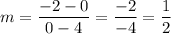
Put the value of te slope and the value of the y-intercept to the equation of a line:

`y=(1)/(2)x+(-2)=(1)/(2)x-2`

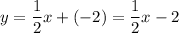
Determine f(8).

Put x = 8 to the equation of a line:

`f(8)=(1)/(2)(8)-2=4-2=2`

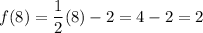
If there is a horizontal shift of 10 to the left, then we have a new line:

`g(x)=f(x+10)`

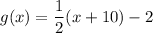`g(x)=(1)/(2)(x+10)-2` use the distributive property

`g(x)=(1)/(2)x+\left((1)/(2)\right)(10)-2=(1)/(2)x+5-2=(1)/(2)x+3`

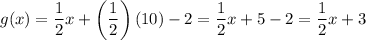
Calculate g(8):

`g(8)=(1)/(2)(8)+3=4+3=7>0`