Step-by-step explanation:
The given data is as follows.
Tank volume (V) = 380 L = 0.38
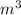
Initial pressure (
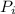 ) = 3 bar
) = 3 bar
Temperature (t) =
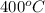
Outlet mass flow rate (
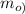 ) = 0.005 kg/s
) = 0.005 kg/s
Final mass (
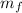 ) =
) =
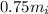
First, we will calculate the initial mass as follows.
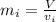
=
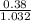
= 0.368 kg
and,
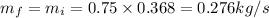
also,
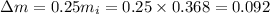
As,
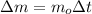
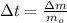
=
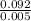
= 18.4 s
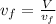
=
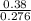
= 1.376
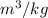
According to the table A-4, value of pressure at
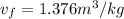 and T =
and T =
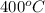 is 2.5 bar.
is 2.5 bar.
Therefore, value of
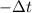 is 18.4 s,
is 18.4 s,
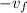 is 1.376
is 1.376
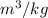 and
and
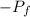 is 2.5 bar.
is 2.5 bar.