Answer:
Solutions : x=4,-2
Extraneous solution : x=-2.
Explanation:
The given equation is
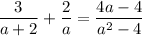
Taking LCM we get
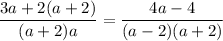
![[\because a^2-b^2=(a-b)(a+b)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/xbhcwlrfo7kf4y1o6pg14saeftv57nmmss.png)
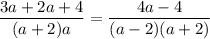
Cancel out common factors from the denominators.
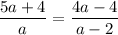
On cross multiplication we get
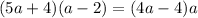
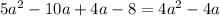

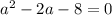
Splitting the middle term we get
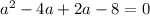
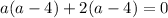

Using zero product property we get
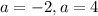
Extraneous solutions: From the solutions of an equation, the invalid solutions are known as extraneous solutions.
For a=-2 right hand side of the given equation is not defined because the denominator become 0.
Therefore, -2 is an extraneous solution.