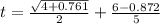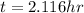Question

Mr. Aydlett is on an island 2 miles offshore and wishes to reach a coastal village 6 miles down a straight shoreline from the point on shore nearest the island. He can row his boat 2 mph and can walk 5 mph. Where should he land his boat to reach the village in the least amount of time? What is the minimum time?

Answer 1

Answer:t=2.11 hr

Explanation:

Given

Aydlett is 2 miles offshore and village is 6 miles down a straight line from the Point on the shore nearest the island

Person can row boat at 2 mph in water and can walk 5 mph in land

Let us suppose Person land the boat at a x miles from Point on the shore

thus time taken by him to reach

`t_1=(√(x^2+2^2))/(2)`

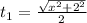
Time taken person to reach village by land is

`t_2=(6-x)/(5)`

total time
`=(√(x^2+2^2))/(2)+(6-x)/(5)`

we need the time to be least so differentiate t w.r.t to x

`\frac{\mathrm{d} t}{\mathrm{d} x}=(2x)/(2\cdot 2\cdot √(4+x^2))-(1)/(5)`

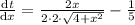
Equating Above term to zero to get minimum time

`(x)/(2√(4+x^2))=(1)/(5)`

`25x^2=16+4x^2`

`x=(4)/(√(21))`

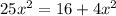
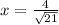
Substituting x in time equation

`t=(√(4+0.761))/(2)+(6-0.872)/(5)`

`t=2.116 hr`