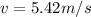Question

A meter stick is held vertically with one end on the floor and is then allowed to fall. Find the speed of the other end just before it hits the floor, assuming that the end on the floor does not slip. (Hint: Consider the stick to be a thin rod and use the conservation of energy principle.)

Answer 1

`v = 5.42 m/s`

Step-by-step explanation:

Let the meter stick will rotate here with its other end fixed

So we will have

`(1)/(2)I\omega^2 = mgh`

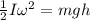
here we know that

h = displacement of center of mass

so we have

`(1)/(2)((m(L)^2)/(3))\omega^2 = mg((L)/(2))`

so we have

`(mL^2\omega^2)/(6) = (mgL)/(2)`

`\omega = \sqrt{(3g)/(L)}`

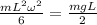
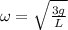
now we need to find the speed of the other end

so we have

`v = L\omega`

`v = √(3gL)`

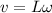
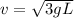
L = 1 m

`v = 5.42 m/s`