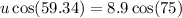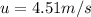Question

An Olympic diver springs off of a high dive that is 3 m above the surface of the water. When she lands in the water she is traveling at a speed of 8.90 m/s at an angle of 75.0° with respect to the horizontal. What was her take off speed and direction, up from the horizontal?

Answer 1

Answer:
`u=4.51 m/s\ at\ angle\ of\ \theta =59.34^(\circ)`

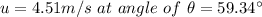
Step-by-step explanation:

Given

height of building h=3 m

Landing velocity of diver
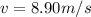`v=8.90 m/s` at an angle of
`75^(\circ)`

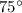
Let u be the initial velocity of diver at an angle of \theta with horizontal

Since there is no acceleration in horizontal direction therefore horizontal component of velocity will remain same

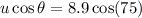`u\cos \theta =8.9\cos (75)` ---- -----1

Considering Vertical motion

`v^2-u^2=2as`

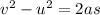
here
`v=8.9\sin (75)`

`u=u\sin \theta`

`s=3 m`

`a=9.8 m/s^2`

`(8.9\sin (75))^2-(u\sin \theta )^2=2* 9.8* 3`

`u\sin \theta =√((8.9\sin 75)^2-(2\cdot 9.8\cdot 3))`

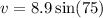
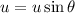
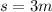
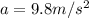
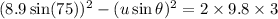
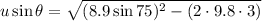
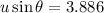`u\sin \theta =3.886` ----------------2

Divide 2 and 1 we get

`\tan \theta =(3.886)/(8.9\cos (75))`

`\tan \theta =1.687`

`\theta =59.34^(\circ)`

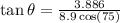
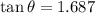
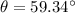
Thus
`u\cos (59.34)=8.9\cos (75)`

`u=4.51 m/s`