Answer:
Mean = 0.17
Variance = 0.0068
Explanation:
It is given in the question that the data is uniformly distributed, therefore the mean will be calculated using the formula
Mean =
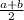
here, a is the minimum value and b is the maximum value
for the data: 0.15, 0.16, 0.17, 0.18, and 0.19
a = 0.15
b = 0.19
Therefore,
Mean =
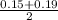
or
Mean =
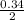
or
Mean = 0.17
Variance =
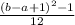
or
Variance =

or
Variance = 0.0068